Last couple of days we have been running a coffee and cake fueled Be-In/Hackfest to learn Python at CSIRO CMAR. In the oceanography community a lot of coding goes on, the large models are written in Fortran and C. The throw-away prototyping is done in Matlab by physical oceanographers and in R by biologists.
R is open source and contribution/hacking friendly, but Matlab is another story altogether. Matlab however has a rich set of documentation and toolboxes which you will probably never read or use, just like you will never redline the tacho in your car - but one gets the comfortable feeling of knowing it is there in case something goes wrong. I was aiming for positive reviews like these.
In my true UI's are the best fashion I did a short IDE round up which you can find here. I learnt a lot about requirements of true large data processing, caveats in python and some backend magic for matplotlib. Also got a chance to look at the scripting API for Java and the pains with the SPI service registries and the death of com.sun.
Since we are on the Python topic I mucked around with running Matlab style functions from Python via Scilab (Java Matlab look alike). Data gets passed around Python Interpreter to Java VM for the sake of syntactic familiarity. After a couple of build hick-ups:

In [81]: from numpy.linalg import pinv,inv
In [82]: from scilab import scilab as sci
In [83]: x = sci.rand(100,100)
In [84]: from pylab import imshow,show
In [85]: a = inv(x)
In [86]: b = pinv(x)
In [87]: c = sci.inv(x)
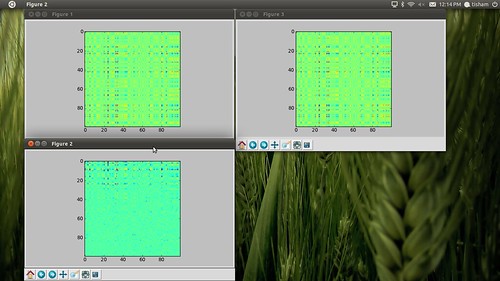
In [88]: figure(1)
In [89]: imshow(a-b)
In [90]: figure(2)
In [91]: imshow(a-c)
In [92]: figure(3)
In [93]: imshow(b-c)
The inverse calculation is a fairly complex series of floating point operations and errors accumulate between the different techniques in the order of 4x10^-15 for the random array. No wonder results from matlab don't match up with those from Scilab and Numpy. Next I will grab a copy of Matlab and use mlabwrap to compare with the "real matlab" computed inverses.
PS: mlabwrap results are in, how do I tell which inverse is more "correct" suggestions welcome.
In [42]: mean(abs(sci.inv(x)-mlab.inv(x)))
Out[42]: 1.0797192783948417e-14
In [43]: mean(abs(sci.inv(x)-inv(x)))
Out[43]: 1.1512191793925341e-15
In [44]: mean(abs(inv(x)-mlab.inv(x)))
Out[44]: 1.0661985412661976e-14
R is open source and contribution/hacking friendly, but Matlab is another story altogether. Matlab however has a rich set of documentation and toolboxes which you will probably never read or use, just like you will never redline the tacho in your car - but one gets the comfortable feeling of knowing it is there in case something goes wrong. I was aiming for positive reviews like these.
In my true UI's are the best fashion I did a short IDE round up which you can find here. I learnt a lot about requirements of true large data processing, caveats in python and some backend magic for matplotlib. Also got a chance to look at the scripting API for Java and the pains with the SPI service registries and the death of com.sun.
Since we are on the Python topic I mucked around with running Matlab style functions from Python via Scilab (Java Matlab look alike). Data gets passed around Python Interpreter to Java VM for the sake of syntactic familiarity. After a couple of build hick-ups:
- locating includes due to scilab layout on Ubuntu
- launching with jvm and libjava on LD_LIBRARY_PATH
- proper setting of SCI env variable to /usr/share/scilab


In [81]: from numpy.linalg import pinv,inv
In [82]: from scilab import scilab as sci
In [83]: x = sci.rand(100,100)
In [84]: from pylab import imshow,show
In [85]: a = inv(x)
In [86]: b = pinv(x)
In [87]: c = sci.inv(x)
In [88]: figure(1)
In [89]: imshow(a-b)
In [90]: figure(2)
In [91]: imshow(a-c)
In [92]: figure(3)
In [93]: imshow(b-c)
The inverse calculation is a fairly complex series of floating point operations and errors accumulate between the different techniques in the order of 4x10^-15 for the random array. No wonder results from matlab don't match up with those from Scilab and Numpy. Next I will grab a copy of Matlab and use mlabwrap to compare with the "real matlab" computed inverses.
PS: mlabwrap results are in, how do I tell which inverse is more "correct" suggestions welcome.
In [42]: mean(abs(sci.inv(x)-mlab.inv(x)))
Out[42]: 1.0797192783948417e-14
In [43]: mean(abs(sci.inv(x)-inv(x)))
Out[43]: 1.1512191793925341e-15
In [44]: mean(abs(inv(x)-mlab.inv(x)))
Out[44]: 1.0661985412661976e-14

No comments:
Post a Comment